Piezoelectric actuators (PEAs) emerged in industry due to their high-precision and stiffness . They convert electrical signals into tiny, precise movements useful in fields like biological cell manipulation (injections) and aerospace (actuation systems) . Their applications also extend to optical focus mechanisms and vibration control. PEAs have limitations. Vibrations occur at high frequencies. Creep causes drift while the hysteresis reduces the tracking accuracy. Material changes or control strategies can address these issues, but there are trade-offs.

Hysteresis models can be broadly classified into two categories: physics-based and mathematical models. Physics-based models are more complex and depend on the specific material properties, making them well-suited for describing phenomena like ferromagnetic hysteresis. Mathematical models, on the other hand, can be further divided into two subcategories: operator-based and differential equation-based. While these models can be adapted to handle asymmetric hysteresis, they come with drawbacks. First, solving them numerically can be computationally expensive, often requiring complex algorithms at each step. Second, incorporating asymmetry often increases the number of parameters needed, making it difficult to find a good fit for the data.

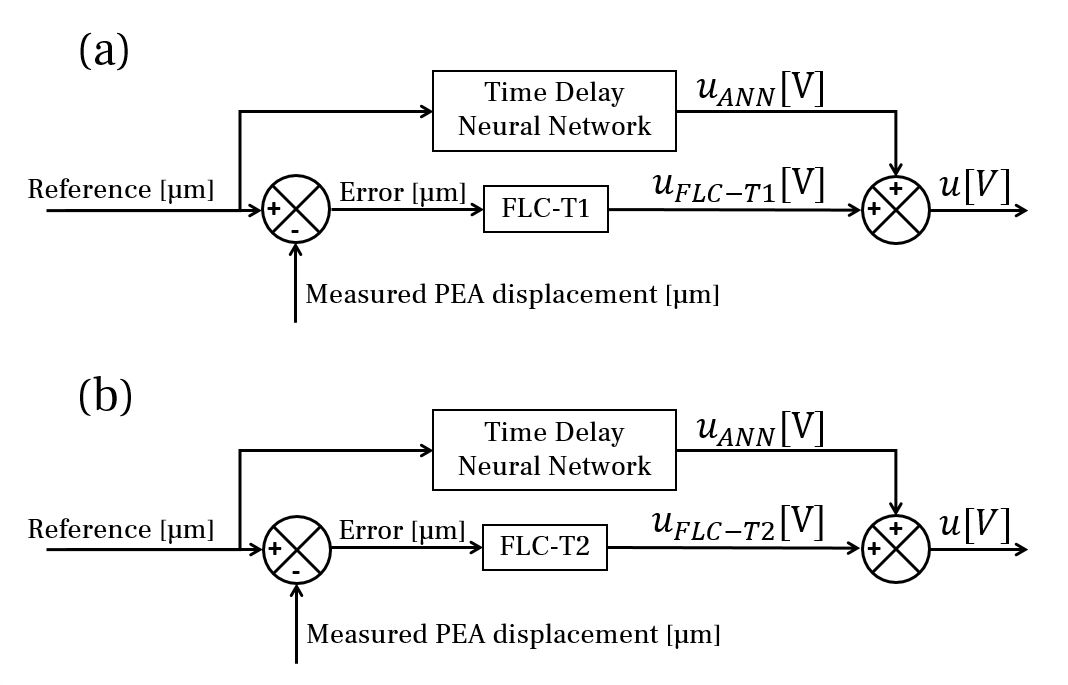
Our research suggested that Artificial Neural Networks (ANNs) offer a more attractive alternative to these mathematical models. ANNs have been shown to be more accurate and easier to implement. Therefore, we believe that ANNs are a suitable choice for implementing feedforward compensation in this study. As to compensate the error in a feedback loop, we used fuzzy logic. This is an easy understanding type of structure because it is expressed through linguistic rules that can be tuned according to the knowledge of a particular system. The designs were implemented with type-1 and type-2 structures.

There are several challenges with traditional fuzzy logic control type-1 (FLC-T1). First, defining the fuzzy rules can be subjective and depend on the expertise of the designer. Second, real-world data often contains noise and inaccuracies. These factors can make the membership functions in type-1 imprecise. To address these limitations, Type-2 Fuzzy Logic control structures (FLC-T2) was developed. FLC-T2 can handle uncertainties in the system better than FLC-T1. This means it can adapt to situations where the exact rules or data are unclear. As a result, FLC-T2 is generally more robust than FLC-T1.

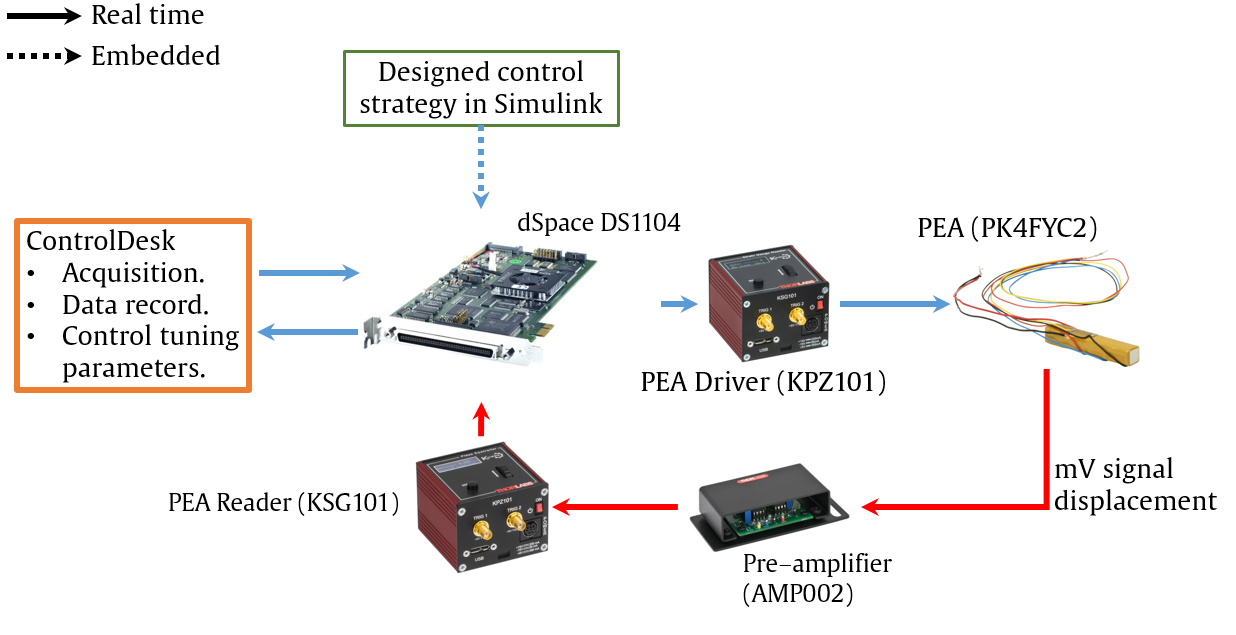
We used a real-time platform designed to fine-tune controls for optimal performance. All the control structures were designed in Matlab/Simulink and embedded in a dSPACE platform. The reference signals were triangular with an amplitude of the maximum allowed voltage and a 4s period. The actuator (PEA) was a Thorlabs PK4FYC2, a stack actuator with linear movement achieved through layers of piezoelectric material (PZT) bonded with epoxy and glass beads. For accurate displacement readings, the manufacturer included a strain gauge based on a Wheatstone bridge. The PEA moved within a range of 0-38.5 micrometers with a 0-150 Volt input. The manufacturer reported a maximum displacement error of 15% due to hysteresis. A schematic of the peripheral hardware is shown in Fig. 2.

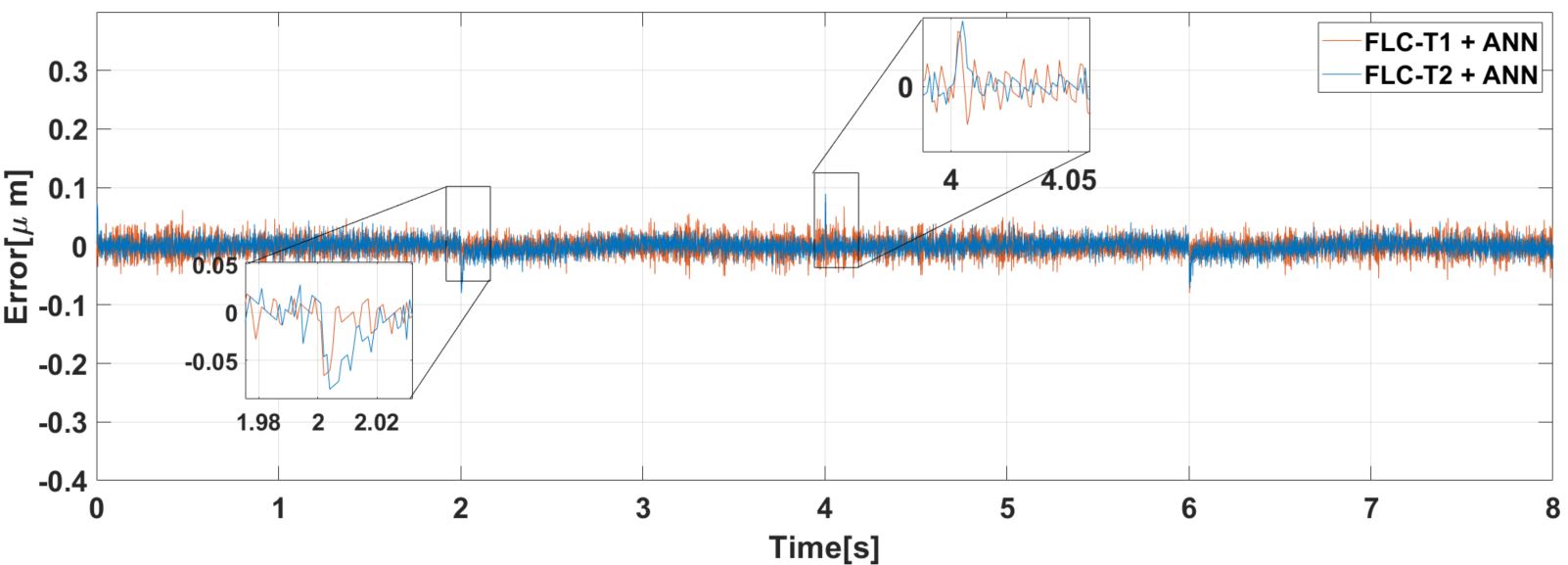
The results show a suitable error tracking that is seen in Fig. 3. Specially every 2s (due to period), the slope sign changes and it is displayed a variation less than 0.1 μm around the null value. At the first slope sign shift at 2s, both controllers behaved similarly although the FLC-T1-ANN, seems to have a slightly faster correction. Oppositely, when the slope switches from negative to positive at 4s, the situation has a modest change where the FLC-T2-ANN compensates the error. On the other sides, it can be seen that the FLC-T2-ANN has a suitable performance due to the error amplitude which lower than the alternative option. In regards to the metrics, we used the integral of the absolute error (IAE). Although the magnitudes are similar, FLC-T1-ANN showed the lower values in overall and thus it was used as a reference for the percentage calculation. The FLC-T2-ANN achieved better outcomes since the difference is 21.32% against FLC-T1.